When I learned about principal component analysis (PCA), I thought it would be really useful in big data analysis, but that's not true if you want to do prediction. I tried PCA in my first competition at kaggle, but it delivered bad results. This post illustrates how PCA can pollute good predictors.
When I started examining this problem, I always had following picture in mind. So I couldn't resist to include it. The left picture shows, how I feel about my raw data before PCA. The right side represents how I see my data after applying PCA on it.
Yes it can be that bad …
The basic idea behind PCA is pretty compelling:
Look for a (linear) combination of your variables which explains most of the variance of the data. This combination shall be your first component. Then search for the combination which explains the second most of the variance and is vertical to the first component.
I don't want to go into details and assume that you are familiar with the idea.
At the end of the procedure you have uncorrelated variables, which are linear combinations of your old variables. They can be ordered by how much variance they explain. The idea for machine learning / predictive analysis is now to use only the ones with high variance, because variance equals information, right?
So we can reduce dimensions by dropping the components which do not explain much of the variance. Now you have less variables, the dataset becomes manageable, your algorithms run faster and you have the feeling, that you have done something useful to your data, that you have aggregated them in a very compact but effective way.
It's not as simple as that.
Well let's try it out with some toy data.
At first we build a toy data set. Therefor we first create some random “good” x values, which are simply drawn from a normal distribution. The response variable y is a linear transformation of x, with a random error, so we should be able to make a good prediction of y with the help of good_x.
The second covariable is a “moisy” x, which is highly correlated with good_x, but has more variance itself.
To build a bigger dataset I included variables which are very useless for predicting y, because they are randomly normal distributed with mean zero. Five of the variables are highly correlated and the other five as well, which will be detected by the PCA later.
library("MASS")
set.seed(123456)
### building a toy data set ###
## number of observations
n <- 500
## good predictor
good_x <- rnorm(n = n, mean = 0.5, sd = 1)
## noisy variable, which is highly correlated with good predictor
noisy_x <- good_x + rnorm(n, mean = 0, sd = 1.2)
## response variable linear to good_x plus random error
y <- 0.7 * good_x + rnorm(n, mean = 0, sd = 0.11)
## variables with no relation to response 10 variables, 5 are always
## correlated
Sigma_diag <- matrix(0.6, nrow = 5, ncol = 5)
zeros <- matrix(0, nrow = 5, ncol = 5)
Sigma <- rbind(cbind(Sigma_diag, zeros), cbind(zeros, Sigma_diag))
diag(Sigma) <- 1
random_X <- mvrnorm(n = n, mu = rep(0, 10), Sigma = Sigma)
colnames(random_X) <- paste("useless", 1:10, sep = "_")
## binding all together
dat <- data.frame(y = y, good_x, noisy_x, random_X)
## relationship between y and good_x and noisy_x
par(mfrow = c(1, 2))
plot(y ~ good_x, data = dat)
plot(y ~ noisy_x, data = dat)
Obviously, good_x is a much better predictor for y than noisy_x.
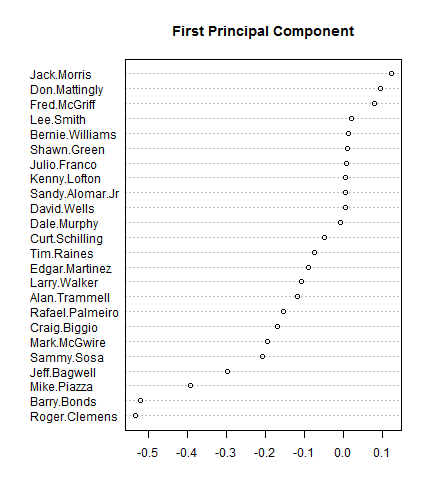
Now I run the principal component analysis. The first three components explain a lot, which is due to the way I constructed the data. The variables good_x and noisy_x are highly correlated (Component 3), the useless variables number one to five are correlated and so are the useless variables number six to ten (Components 1 and 2)
## pca
prin <- princomp(dat[-1], cor = TRUE)
## results visualized
par(mfrow = c(1, 2))
screeplot(prin, type = "l")
loadings(prin)
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 Comp.9
## good_x 0.700 0.148 0.459 -0.441
## noisy_x 0.700 0.148 -0.424 0.474
## useless_1 -0.183 -0.408 -0.290 -0.464 0.382 -0.184 0.180
## useless_2 -0.204 -0.390 0.170 0.490 0.549 0.114 -0.116
## useless_3 -0.228 -0.393 0.242 -0.434 0.176
## useless_4 -0.201 -0.394 -0.446 -0.278 0.309 -0.103 0.599
## useless_5 -0.172 -0.414 0.365 -0.271 0.105 -0.306 -0.484
## useless_6 0.413 -0.172 0.209 -0.527 -0.125
## useless_7 0.411 -0.171 -0.305 0.273 0.398 -0.311 0.413
## useless_8 0.368 -0.241 -0.424 0.340 -0.252 -0.403 -0.209 -0.447
## useless_9 0.398 -0.191 0.366 0.386 -0.166 0.427 0.262
## useless_10 0.405 -0.215 0.137 -0.157 0.122 -0.297
## Comp.10 Comp.11 Comp.12
## good_x -0.234 0.146
## noisy_x 0.239
## useless_1 0.144 -0.440 -0.252
## useless_2 0.272 -0.284 0.196
## useless_3 0.264 0.561 0.347
## useless_4 -0.237
## useless_5 -0.443 -0.220
## useless_6 0.186 -0.392 0.515
## useless_7 0.412 0.165
## useless_8 -0.135 0.150
## useless_9 -0.416 -0.166 -0.171
## useless_10 0.484 0.212 -0.596
##
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## SS loadings 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## Proportion Var 0.083 0.083 0.083 0.083 0.083 0.083 0.083 0.083
## Cumulative Var 0.083 0.167 0.250 0.333 0.417 0.500 0.583 0.667
## Comp.9 Comp.10 Comp.11 Comp.12
## SS loadings 1.000 1.000 1.000 1.000
## Proportion Var 0.083 0.083 0.083 0.083
## Cumulative Var 0.750 0.833 0.917 1.000
dat_pca <- as.data.frame(prin$scores)
dat_pca$y <- y
plot(y ~ Comp.3, data = dat_pca)
Now we can compare the prediction of y with the raw data and with the data after pca analysis. The first method is a linear model. Since the true relationship between good_x and y is linear, this should be a good approach. At first we take the raw data and include all variables, which are the good and the noisy x and the useless variables.
As expected, the linear model performs very well with an adjusted R-squared of 0.975. The estimated coefficient of good_x is also very close to the true value. The linear model also performed well on finding the only covariable that matters indicated by the p-values.
## linear model detects good_x rightfully as only good significant
## predictor
mod <- lm(y ~ ., dat)
summary(mod)
##
## Call:
## lm(formula = y ~ ., data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.3205 -0.0750 -0.0048 0.0784 0.3946
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.001377 0.005681 -0.24 0.81
## good_x 0.705448 0.006411 110.03 <2e-16 ***
## noisy_x -0.002980 0.004288 -0.70 0.49
## useless_1 -0.010783 0.006901 -1.56 0.12
## useless_2 0.009326 0.006887 1.35 0.18
## useless_3 -0.001307 0.007572 -0.17 0.86
## useless_4 -0.005631 0.007037 -0.80 0.42
## useless_5 0.002154 0.007116 0.30 0.76
## useless_6 -0.001407 0.007719 -0.18 0.86
## useless_7 -0.003830 0.007513 -0.51 0.61
## useless_8 0.004877 0.007215 0.68 0.50
## useless_9 0.000769 0.007565 0.10 0.92
## useless_10 0.005247 0.007639 0.69 0.49
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.112 on 487 degrees of freedom
## Multiple R-squared: 0.976, Adjusted R-squared: 0.975
## F-statistic: 1.62e+03 on 12 and 487 DF, p-value: <2e-16
##
But we wanted to use PCA for dimensionality reduction. The screeplot some plots above suggests, that we should take the first four components, because they explain most of the variance. Applying the linear model on the reduced data gives us a worse model. The adjusted R-squared drops to 0.787.
dat_pca_reduced <- dat_pca[c 1=""Comp.1"," 2=""Comp.2"," 3=""Comp.3"," 4=""Comp.4")" language="("y","][/c]
mod_pca_reduced <- lm(y ~ ., data = dat_pca_reduced)
summary(mod_pca_reduced)
##
## Call:
## lm(formula = y ~ ., data = dat_pca_reduced)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.9634 -0.2188 -0.0147 0.2084 0.9651
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.35828 0.01463 24.50 < 2e-16 ***
## Comp.1 0.03817 0.00786 4.86 1.6e-06 ***
## Comp.2 -0.00778 0.00795 -0.98 0.33
## Comp.3 0.48733 0.01149 42.41 < 2e-16 ***
## Comp.4 0.11190 0.02138 5.24 2.4e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.327 on 495 degrees of freedom
## Multiple R-squared: 0.789, Adjusted R-squared: 0.787
## F-statistic: 463 on 4 and 495 DF, p-value: <2e-16
##
The first random forest with the raw data gives the best results with 93.15% of the variance explained. This result is not as good as the linear model, because the true relationship is linear, but it is still a reasonable result.
library("randomForest")
## raw data
set.seed(1234)
forest <- randomForest(y ~ ., data = dat)
forest
##
## Call:
## randomForest(formula = y ~ ., data = dat)
## Type of random forest: regression
## Number of trees: 500
## No. of variables tried at each split: 4
##
## Mean of squared residuals: 0.03436
## % Var explained: 93.15
## pca data
set.seed(1234)
forest_pca <- randomForest(y ~ ., data = dat_pca)
forest_pca
##
## Call:
## randomForest(formula = y ~ ., data = dat_pca)
## Type of random forest: regression
## Number of trees: 500
## No. of variables tried at each split: 4
##
## Mean of squared residuals: 0.07293
## % Var explained: 85.47
As suspected we loose again predictive power and the explained variance drops to 70.98 %.
That's a difference of about 22% percent of explained variance, compared to the results from the random forest with the raw data.
## reduced pca data
set.seed(1234)
forest_pca <- randomForest(y ~ ., data = dat_pca_reduced)
forest_pca
##
## Call:
## randomForest(formula = y ~ ., data = dat_pca_reduced)
## Type of random forest: regression
## Number of trees: 500
## No. of variables tried at each split: 1
##
## Mean of squared residuals: 0.1456
## % Var explained: 70.98
Of course PCA still is a useful statistical tool. It can help as a descriptive tool or if you are looking for some latent variable behind your observed features (which is very common in surveys) it does its job. But don't use it blindly in predictive models.
This blog entry was inspired by this one:
http://blog.explainmydata.com/2012/07/should-you-apply-pca-to-your-data.html
I am interested in your experience with PCA. Feel free to comment.
R-bloggers.com offers daily e-mail updates about R news and tutorials on topics such as: visualization (ggplot2, Boxplots, maps, animation), programming (RStudio, Sweave, LaTeX, SQL, Eclipse, git, hadoop, Web Scraping) statistics (regression, PCA, time series,ecdf, trading) and more...